This is the second in a series of four blog posts to introduce the underpinning concepts related to variation in systems. In the first post we discussed common cause and special cause variation. In this post, we explain that a stable system is predictable. This is an edited extract from our book, Improving Learning.

System stability

System stability relates to the degree to which the performance of any system is predictable — that the next data point will fall randomly within the natural limits of variation.

A formal definition can provide a useful starting point for exploring this important concept.

A system is said to be stable when the observations fall randomly within the natural limits of variation for that system and conform to a defined distribution, frequently a normal distribution.

All systems exhibit variation in all four types of measures: results, perceptions, processes, and inputs.

Variation within groups

Consider, for example, the student results in Figure 1, which show the reading scores for 103 students attending an Australian high school. Each student was tested as part of NAPLAN when they were in Year 7.

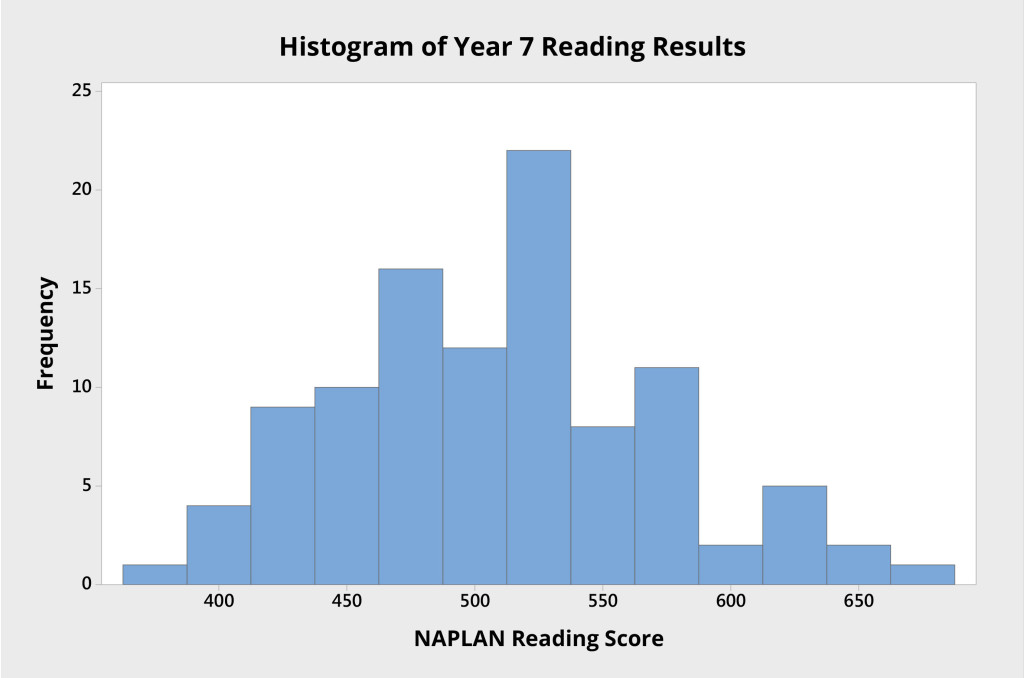
Figure 1 Histogram of Year 7 individual student NAPLAN scores from an Australian high school. — Figure 1 Histogram of Year 7 individual student NAPLAN reading scores from an Australian high school.

The histogram shows the variation in student performance, from which we can see:

the mean score is approximately 510 points; and
the data seem to be roughly normally distributed, as there is a stronger cluster of scores around the mean score, and the curve appears roughly bell shaped.

A stable system produces predictable results within the natural limits of variation for that system.

If we use the histogram to study the variation in student NAPLAN results, we can assume that, if there were additional students in that group, their results would very likely fall within the distribution shown.

Furthermore, if nothing is done to change a stable system, it is rational to predict that future NAPLAN reading performances will be similar, both in the mean or average performance and in the range of variation evident in the results.

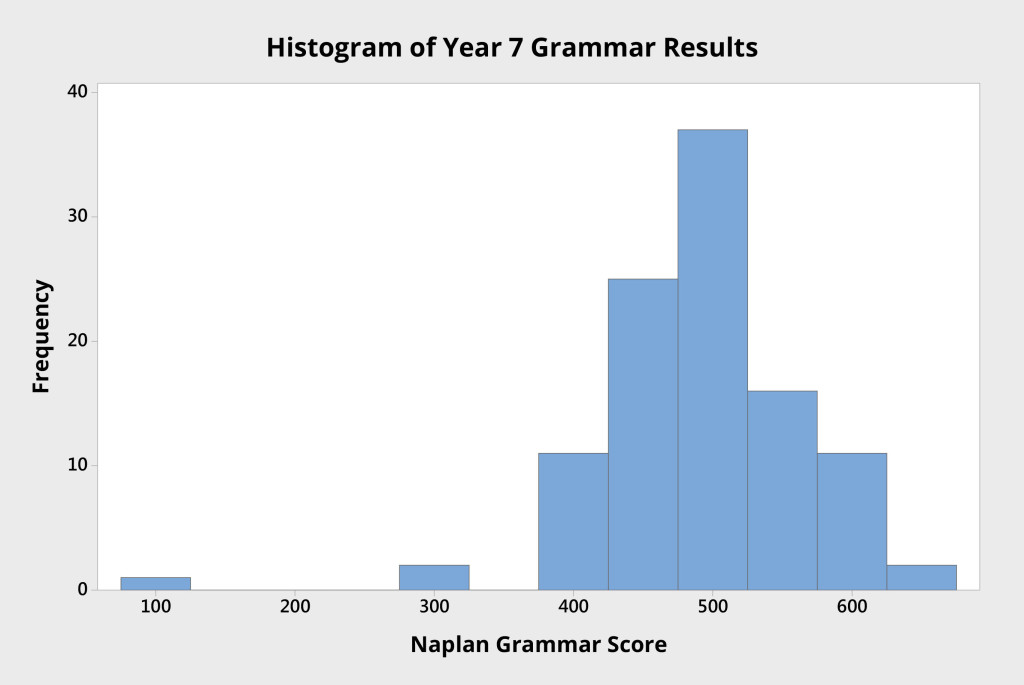
Figure 2 Histogram of Year 7 individual student NAPLAN scores from an Australian high school. — Figure 2 Histogram of Year 7 individual student NAPLAN grammar scores from an Australian high school.

The histogram in Figure 2 shows the grammar scores of the same group of Year 7 students. Here the mean score is about 500 points.

Notice here the presence of a single student with a score of approximately 100. This data point appears to be an outlier: it is noticeably different to the other data points.

One could reasonably assume that this data point represents something out of the ordinary, that the causes that led to this result are different to those experienced by the remainder of the system.

Given that this data point is so different to the others, investigation is called for, and is likely to reveal a specific reason, an assignable cause. Where specific causes can be identified, they are called special causes or assignable causes. In this instance, investigation revealed that this student had scored about 200 points below expectation due to illness on the day of the test.

These examples of system stability, within groups, relate to measures of students’ learning at a particular point in time.

Variation between groups

The variation that is evident between groups is often of great interest. For example, we may be interested in variation between classes of the same grade or year, or between schools in different districts or states.

In these instances, the focus is no longer on variation within a set of data points, but upon differences in variation that is evident between groups (multiple sets) of data points.

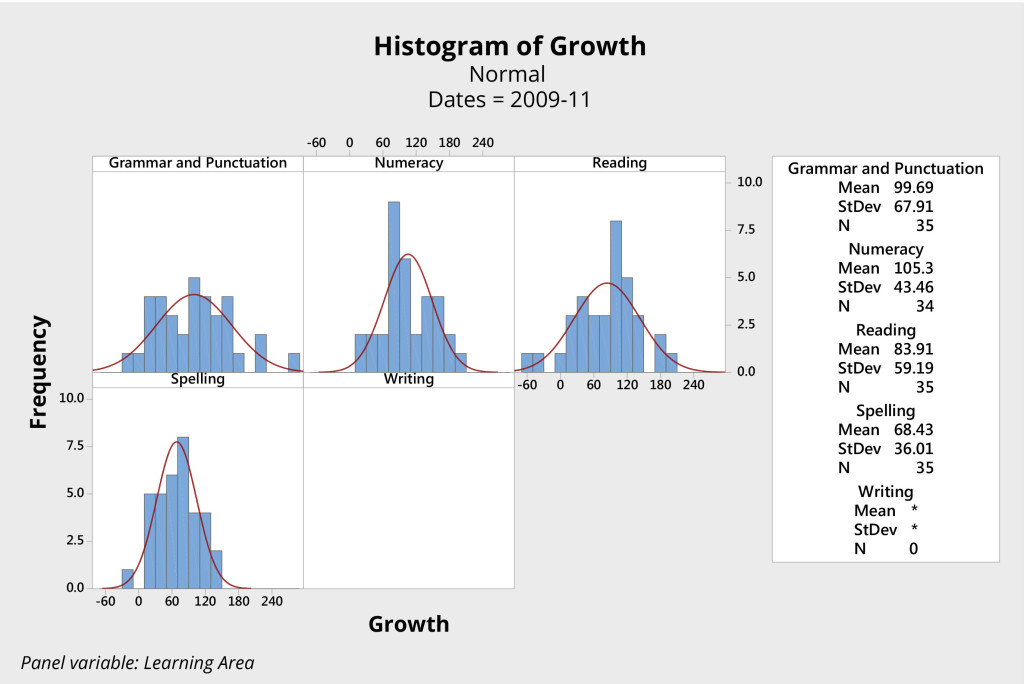
Consider, for example, the sets of histograms presented in Figures 3 and 4. Both come from the same primary school, and both represent the growth in students’ scores in key learning areas, as measured by NAPLAN, over the two-year period from Year 3 to Year 5.

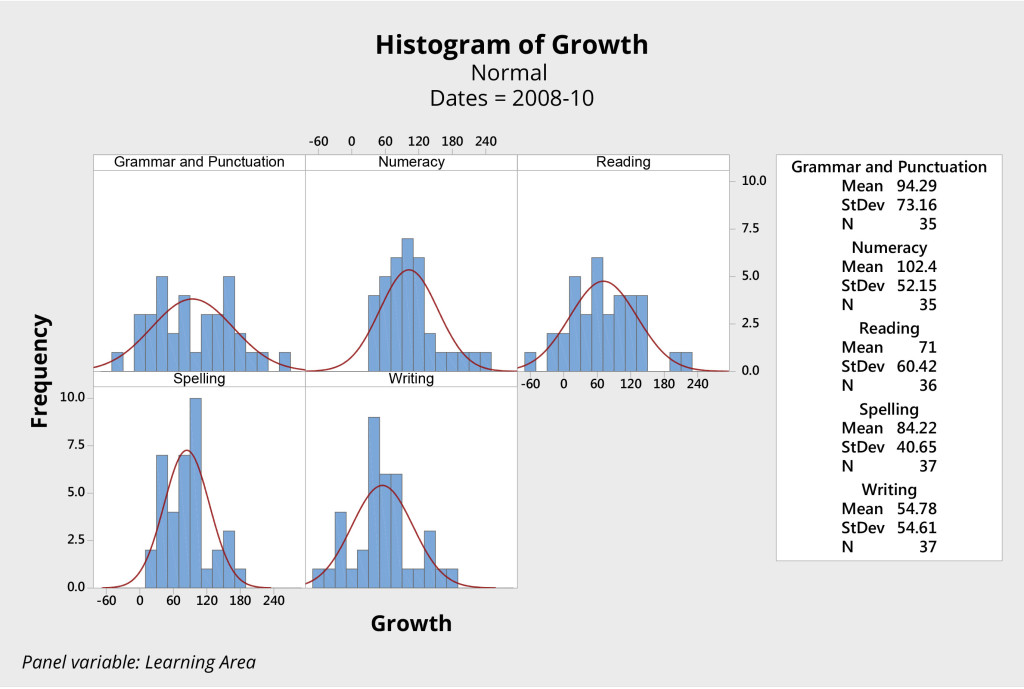
Figure 3. Histograms of student growth literacy and numeracy years 3 to 5, 2008 - 2010, NAPLAN individual student scores from an Australian primary school. — Figure 3. Histograms of student growth literacy and numeracy years 3 to 5, 2008 – 2010, NAPLAN individual student scores from an Australian primary school.

Figure 4. Histograms of student growth literacy and numeracy years 3 to 5, 2009 - 2011, NAPLAN individual student scores from an Australian primary school. — Figure 4. Histograms of student growth literacy and numeracy years 3 to 5, 2009 – 2011, NAPLAN individual student scores from an Australian primary school.

The first group of students (Figure 3) was initially tested in 2008, when the students were in Year 3. This same group of students was tested again in 2010, when they were in Year 5. The histograms show the difference, or growth, in scores over that two-year period.

The second group of students (Figure 4) is a year younger. These students were tested in 2009, when they were in Year 3, and again in 2011, when they were in Year 5. (Due to differences in the testing of writing between 2009 and 2011, growth in this area was not evaluated for the second group).

Has one group of students performed better than the other? These data look very similar. Analysis fails to show any significant difference between these two groups of students in either the mean score or variation for each of the four learning areas.

With two different groups of students, this school produced essentially the same results in terms of student growth over the two two-year periods. The data are practically the same for each group, only the names of the students are different.

Consider the scores for grammar and punctuation, for example. For both groups of students, the system produced a mean score of about 95 and a range from approximately -70 to 250. It appears the system produced consistent results with a mean growth of approximately 95 points and natural limits of variation plus or minus approximately 160. The story is similar for the other three learning areas.

We can reasonably predict that, unless something changes significantly at this school, the next group of students will again produce almost identical results.

The system is thus said to be stable — the points fall predictably between the natural limits of variation for the system.

Variation over time

Outliers, trends and unusual observations in time-series data can indicate the presence of special cause variation. Where these exist, the system is not stable.

So far we have used the histogram to help us to study variation in a system. We can also study system variation by plotting data as a time series using a run chart (line graph) or control chart as in Figure 5. Here the class total of correct spelling words per week is plotted over weekly intervals.

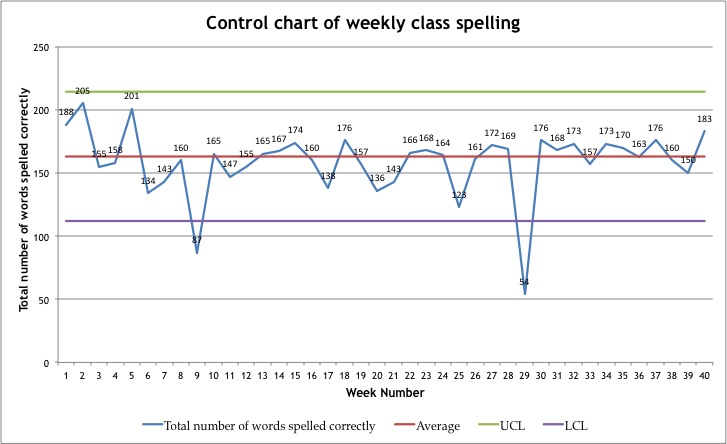
Figure 5. Control Chart of weekly class spelling total.

Notice the dips in the number of correct words at weeks nine and twenty-nine. One could reasonably seek explanations and learn that it was, for example, the week of the school camp, or an outbreak of influenza that lead to student absences resulting in lower numbers of correct words. These would be examples of special cause variation.

Instances of special cause variation in time series data can be revealed by patterns or trends in the data, including:

a series of consecutive data points that sequentially improve or deteriorate; and
an uncommonly high number of data points above or below the average.

If there is an unexplained pattern in the data, this is evidence of special cause variation and investigation is justified. Such a system is said to be unstable.

If special cause variation is absent, future performance can be predicted with confidence. This performance will fall within the natural limits of variation for that process. If special cause variation is absent, or the presence of any special causes is explained, and system performance can be confidently predicted, the system is said to be stable.

Where unusual data points or trends have not been explained, any predictions of future performance will be less reliable. In such cases, the system is said to be unstable. Confident prediction is not possible for an unstable system.

In the next post in this series, we explain the notion of system capability. These concepts, stability and capability, along with an understanding of common cause and special cause variation, discussed in the pervious post, are fundamental to preventing tampering with systems. Tampering is a common practice in school education systems (and elsewhere), and usually makes things worse!

Read about four types of measures, and why you need them.

Read about common cause and special cause variation.

Read more in our comprehensive resource: IMPROVING LEARNING – A how-to guide for school improvement.

Purchase our learning and improvement guide Using data to improve.